Origine du champ magnétique terrestre - plus de détails
Pour décrire exhaustivement la cause du champ magnétique terrestre, on doit résoudre des équations simultanées qui décrivent les conditions électromagnétiques et thermiques dans le noyau de la Terre. Dans Merrill et al. (1998), on énumère dix de ces équations : les équations de Maxwell qui décrivent les interactions entre les champs magnétiques et les courants électriques, l'équation de Navier-Stokes qui décrit le mouvement du liquide dans le noyau externe et les équations qui décrivent le potentiel gravitationnel, le flux thermique et plusieurs autres paramètres. à son tour, chaque équation dépend de conditions aux limites et des valeurs initiales attribuées à la conduction qui, souvent, sont mal connues.
On peut avoir une bonne compréhension de la physique du phénomène en considérant l'équation de l'induction magnétique :
où B est le vecteur champ magnétique, v le vecteur vitesse, t le temps, F la conductivité et μ la perméabilité magnétique, égale à μ0 dans ce cas.
Le premier terme du côté droit correspond à l'interaction entre le champ magnétique et un conducteur en mouvement, ce qui cause l'accroissement ou la diminution du champ magnétique. Le second terme du côté droit représente la diffusion.
Si la vitesse est nulle, le premier terme du côté droit disparaît. Le terme restant implique qu'en l'absence d'un conducteur en mouvement, le champ magnétique s'estomperait exponentiellement, sur une période d'environ 15 000 ans.
Si l'on suppose que le liquide est un conducteur parfait, et donc le deuxième terme est égal à zéro (σ = ∞). Dans ces conditions, les lignes de champ magnétique sont "gelées" dans le liquide conducteur et se déplacent de concert. Le comportement de ces lignes de champ est important pour comprendre le mécanisme par lequel le champ magnétique est généré.
On doit introduire ici deux concepts : les champs poloïdaux et les champs toroïdaux. Un champ poloïdal (ou transversal) possède une composante radiale. Nous connaissons ce type de champ : les champs dipolaires sont poloïdaux. Par ailleurs, les champs toroïdaux sont en forme de tore ou d'anneau et ne possèdent pas de composante radiale. Dans la Terre, les champs toroïdaux sont confinés au noyau et on ne peut les détecter à la surface. Ils jouent néanmoins un rôle important dans la production du champ géomagnétique.
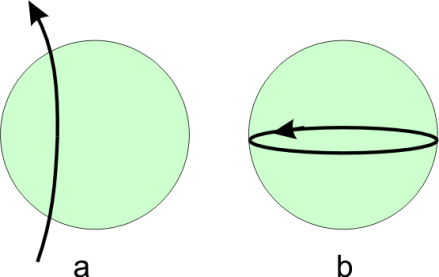
Champs poloïdaux (gauche) et champs toroïdaux (droit)
Supposons que le noyau tourne avec une vitesse angulaire qui dépend de son rayon. Considérons ce qui arrivera à un champ poloïdal dont les lignes de champ sont "gelées" et qui se déplacent donc avec le liquide. Si le liquide se déplace plus lentement dans la partie supérieure du noyau externe, les lignes retarderont par rapport aux lignes plus proches du centre. Après un tour complet, deux boucles toroïdales seront formées, comme le montre le diagramme. C'est ce que l'on appelle l'effet ω, le mécanisme par lequel un champ poloïdal se transforme en un champ toroïdal.
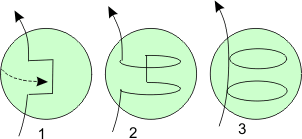
effet ω
Considérons ensuite une ligne d'un champ toroïdal gelé dans une cellule convective ascendante. Les lignes du champ seront tirées par la cellule. La force de Coriolis, qui est une conséquence de la rotation de la Terre, pousse le liquide ascendant à tourner dans le sens inverse des aiguilles d'une montre (dans l'hémisphère Nord). Les lignes de champ seront courbées dans le liquide et, après un quart de tour, on obtiendra une boucle magnétique poloïdale. On appelle ce processus l'effet α, un mécanisme par lequel un champ toroïdal se transforme en champ poloïdal. Les boucles poloïdales peuvent se fondre et produire un champ poloïdal étendu.
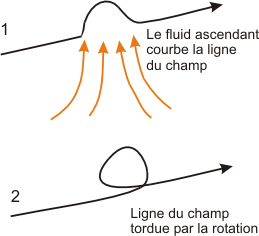
effet α
Pour expliquer comment les effets α et ω peuvent produire le champ géomagnétique, on a proposé plusieurs mécanismes nommés αω, α2 et α2ω. Dans la dynamo αω, la circulation du fluide à travers les lignes du champ poloïdal, un mouvement lié à la rotation différentielle du noyau externe, entraîne la formation d'un champ toroïdal dans le noyau externe. La torsion des lignes du champ toroïdal gelées dans le liquide ascendant crée, à son tour, des champs poloïdaux qui renforcent le champ poloïdal original.
Pour que le champ magnétique demeure continu, en d'autres termes pour que ( ), le taux de génération du champ par le mécanisme αω doit être égal au taux de sa diffusion. Si la génération du champ n'est pas égale à la diffusion, le champ s'accroîtra ou diminuera, ce qui est probablement la situation normale.