Generation of the Earth's magnetic field - In depth
To completely describe how the geomagnetic field is generated it is necessary to solve simultaneous equations describing the electromagnetic and thermal conditions in the Earth's core. Merrill et al (1998) list ten such equations. These include Maxwell's equations which describe the interaction between magnetic fields and electric currents, the Navier-Stokes equation which describes the fluid motion in the outer core, and equations describing the gravity potential, the heat flow, and many other parameters. Each equation is, in turn, dependent on the boundary conditions and the initial conductions chosen. These are often poorly known.
A good deal of physical insight is gained by examining the magnetic induction equation.
B is the magnetic field vector, v is a velocity vector, t is time, F is the conductivity and μ is the magnetic permeability (equal to μ0) in this case.
The first term on the right-hand side represents the interaction between the magnetic field and a moving conductor, which causes build-up (or breakdown) of the magnetic field. The second term on the right-hand side is the diffusion term.
If the velocity is zero, the first term on the right-hand-side disappears. The remaining terms tell us that in the absence of a moving conductor the magnetic field will die away exponentially. The time constant is about 15,000 years.
We can set the second term equal to zero by assuming that the fluid is a perfect conductor (σ = ∞). Under these conditions, magnetic field lines become "frozen" into the conducting fluid, always moving with it. This behaviour of the field lines is important in explaining the mechanism by which the magnetic field is generated.
Two other concepts must be described at this point: poloidal fields and toroidal fields. A poloidal field is one which has a radial component. This is the type of field with which we are all familiar since dipole fields are poloidal. A toroidal field, on the other hand, is ring or donut shaped, with no radial component. In the Earth, toroidal fields are confined to the core and are not detectible at the Earth's surface. Nevertheless they play an important role in the production of the magnetic field.
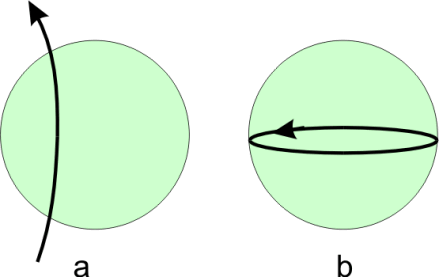
Poloidal field (left) and toroidal field (right)
Suppose that the core rotates with an angular velocity that depends on its radius. Consider what will happen to a poloidal field whose field lines are "frozen in" so that they move along with the fluid. If the fluid is moving more slowly in the upper part of the outer core, those field lines will be left behind compared to field lines closer to the centre. Eventually, after a complete circuit, two toroidal loops will be formed, as shown in the diagram. This is called the ω-effect - a mechanism by which poloidal fields are converted to toroidal fields.
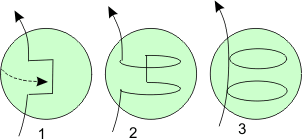
ω-effect
Now consider a field line from a toroidal field, frozen into a rising convective cell. The field line will be pulled along with the cell. Since the Earth is rotating, the Coriolis force will cause the upwelling fluid to rotate counterclockwise (in the northern hemisphere). The field line will be twisted along with the fluid, and after a quarter turn, a poloidal magnetic loop is produced. This process is called the α-effect - a mechanism by which toroidal fields are converted to poloidal fields. The poloidal loops can merge to produce a large poloidal field.
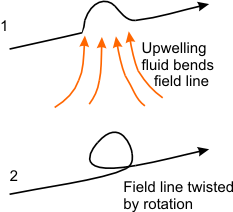
α-effect
Various methods have been proposed by which the α-effect and the ω-effect can generate the Earth's magnetic field. These go by the acronyms αω, α2, α2ω. In the αω dynamo, the motion of the fluid, associated with differential rotation of the outer core, through the poloidal field lines give rise to a toroidal field in the outer core. The twisting of toroidal field lines frozen in upwelling fluid, gives rise, in turn, to poloidal fields which can reinforce the original poloidal field.
To maintain a steady-state magnetic field ( ) the rate at which the field is generated by the αω-effect must equal the rate of diffusion. If they are not equal, the field will either grow or decay, which is probably the normal situation.