Magnetic components
The Earth's magnetic field is a vector quantity; at each point in space it has a strength and a direction. To completely describe it we need three quantities. These may be:
- three orthogonal strength components (X, Y, and Z);
- the total field strength and two angles (F, D, I); or
- two strength components and an angle (H, Z, D)
The relationship between these 7 elements is shown in the diagram.
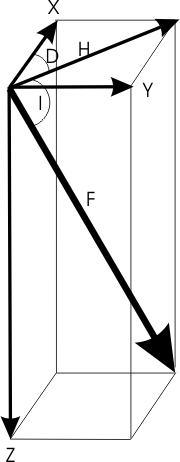
| Component | Description |
|---|---|
| F | the total intensity of the magnetic field vector |
| H | the horizontal intensity of the magnetic field vector |
| Z | the vertical component of the magnetic field vector; by convention Z is positive downward |
| X | the north component of the magnetic field; X is positive northward |
| Y | the east component of the magnetic field; Y is positive eastward |
| D | magnetic declination, defined as the angle between true north (geographic north) and the magnetic north (the horizontal component of the field). D is positive eastward of true North. |
| I | magnetic inclination, defined as the angle measured from the horizontal plane to the magnetic field vector; downward is positive |
D and I are measured in degrees. All other elements are measured in nanotesla (nT; 1 nT = 10-9 Tesla).
The seven elements are related through the following simple expressions.